Para poder entender que una ecuacion cuadratica primero debemos saber que es una ecuacion.
Para resolver las ecuaciones cuadraticas existen diferentes metodos de resolucion para llegar a una o varias repuestas:
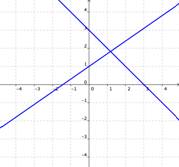
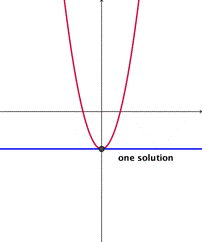
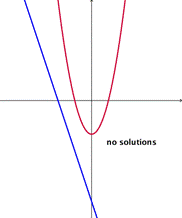
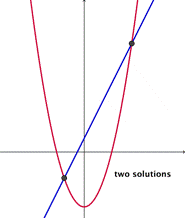
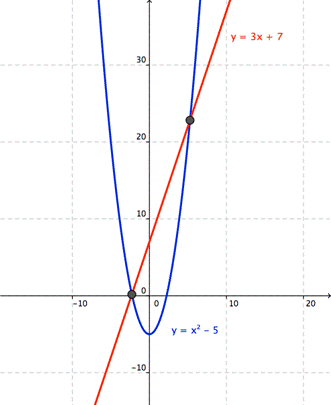
La ecuación completa de segundo grado tiene siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas, dadas por la fórmula
general.
Donde el símbolo "±" indica que los dos valores son soluciones.
¿Qué es una Ecuación?
Es una expresión algebraica que consta de dos miembros separados por un signo de igualdad. Uno o ambos miembros de la ecuación debe tener al menos una variable o letra, llamada incógnita.Una ecuación cuadrática es una ecuación en su forma ax2 + bx + c, donde a, b, y c son números reales.Ejemplo:
9x2 + 6x + 10 a = 9, b = 6, c = 10 3x2 - 9x a = 3, b = -9, c = 0Para resolver las ecuaciones cuadraticas existen diferentes metodos de resolucion para llegar a una o varias repuestas:
1.) METODO DE FORMULA GENERAL:
general.
Resolucion:
Una ves con lo 2 resultados encontrados reemplazamos en la ecuacion original para saber si estos son correctos de la siguiente forma:
como vemos en el siguiente ejemplo ambos resultados son correctos, pero en caso de no salir la comprobacion debemos volver a revisar todo el ejercicio.
2 Metodo de Factorizacion:
¿ Que es la factorizacion?
La factorización es muy importante en el
álgebra. No sólo la aprendemos para
expresar un polimonio como
un producto de factores también la utilizamos para: simplificar expresiones
racionales, efectuar operaciones (suma, resta, multiplicación y división) de
expresiones racionales y resolver ecuaciones e inecuaciones cuadráticas.
existen varios casos de factorización: monomio
como factor común, agrupación, trinomio de segundo grado: caso sencillo y caso general, los casos especiales de factorización: diferencia de cuadrados, cuadrados perfectos, suma de cubos y la diferencia de
cubos. Cada uno de estos casos tiene su
procedimiento.
Trata de practicar mucho la factorización,
debido a que es una herramienta básica.
La práctica te ayudará a factorizar los ejercicios con mayor
rápidez.
2.1 metodo de factorizacion por agrupacion de terminos
Esta técnica nos permite factorizar expresiones que tienen cuatro términos o más aplicando la agrupación de términos en dos o más grupos. Luego se factoriza cada grupo, con el objetivo de encontrar un factor común en cada uno de ellos que se pueda factorizar. Finalmente se utilizan los criterios de factorización de bimonios y trinomios, para terminar el proceso.Ejemplo:
para realizar la comprobacion de este ejercicio realizamos la misma operacion que la anterior solo reemplazamos en la ecuacion original.
2.2 trinomio cuadrado perfecto
Surge de elevar al cuadrado un binomio: Resulta un trinomio con dos términos "cuadráticos" y un término "rectangular", enlazados con una visión geométrica de las áreas de un cuadrado y de rectángulo.
Visualización de la fórmula para un cuadrado y para su trinomio cuadrado perfecto
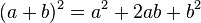
es un trinomio cuadrado perfecto

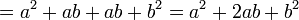
Siendo la regla: el cuadrado de cualquier binomio es igual al cuadrado del primer término, más el doble del producto del primero por el segundo, más el cuadrado del segundo término. De lo anterior resulta que un trinomio será cuadrado perfecto siempre que se cumplan las siguientes condiciones presentadas:
- El polinomio pueda ser ordenado en potencias descendentes de una variable.
- Dos de los términos son cuadrados perfectos.
- El otro término es el doble producto de las raíces cuadradas de los demás.
- El primer y tercer término deben de tener el mismo signo
- En resumen: Se saca la raíz cuadrada del primer y tercer término
 es un TCP si se cumple que el discriminante es cero, es decir, que la cantidad
es un TCP si se cumple que el discriminante es cero, es decir, que la cantidad  es siempre igual a
es siempre igual a  . También se considera un trinomio cuadrado perfecto de la forma:
. También se considera un trinomio cuadrado perfecto de la forma:  , donde las mismas reglas explicadas anteriormente aplican
, donde las mismas reglas explicadas anteriormente aplican